Intro to Game Theory #

Game theory studies how players make strategic decisions. GamesCrafters applies these ideas to non-random two-player games, using computers to discover perfect play and build interactive tools that let anyone explore those strategies.

A 19-year project led by Prof Jonathan Schaeffer used dozens (sometimes hundreds) of computers and AI to prove that Checkers is, in perfect play, a draw. This means that if two perfect players were to play, nobody would ever win!

What Is Game Theory? #

Game theory is the study of strategic decision-making. The outcome for each player depends not only on their own choices, but also on the choices of others. Game theory appears in many fields including economics, political science, psychology, and computer science. In GamesCrafters, we focus on how computational game theory helps us understand and solve games.

Three Categories of Game Theory #

Economic Game Theory #

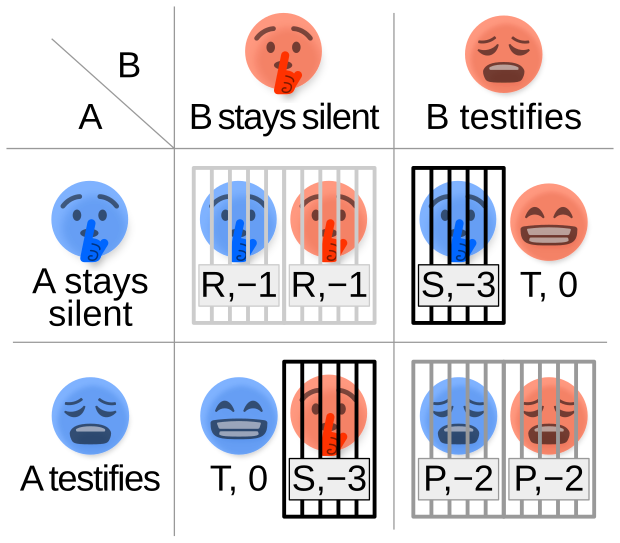
Originating with von Neumann and Morgenstern’s Theory of Games and Economic Behavior (1944), this branch models auctions, negotiations, and strategic dilemmas like the Prisoner’s Dilemma.

• Often involves simultaneous moves
• Information can be incomplete or hidden
• Players try to maximize payoff

Computational Game Theory #

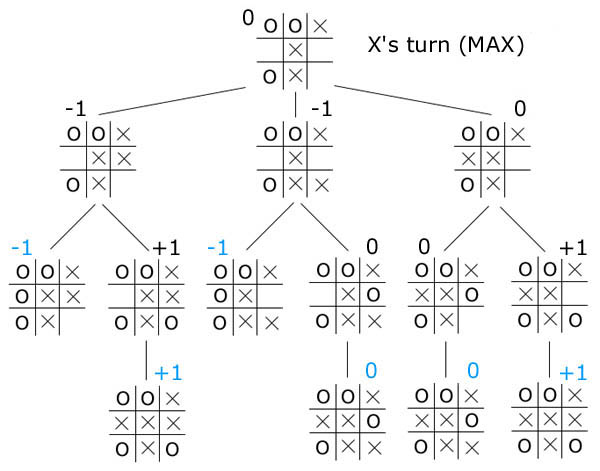
Computational game theory studies games like Tic-Tac-Toe, Connect 4, Othello, or Checkers using algorithms and computing power. This is what we do in GamesCrafters!

• Involves no chance (no dice or shuffled cards)
• Complete information, which means all players know all available information
• Two players alternate moves
• The goal depends on the game (win, avoid losing, make the last move, etc.)

Combinatorial Game Theory #

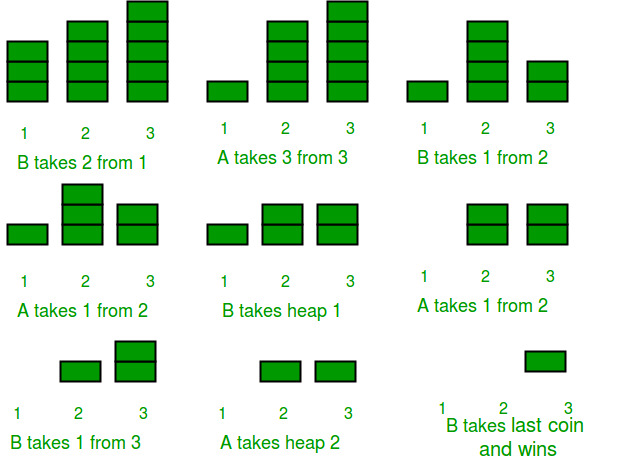
Combinatorial game theory is the mathematical side of games like Nim, Domineering, and Dots-and-Boxes.

• Complete information, alternating moves
• Often, the goal is to make the last move
• Strong connections to number theory and discrete math

What Kind of Board Games Do We Study? #

In GamesCrafters, we focus on a specific class of games:

• No chance, such as dice or shuffled cards
• Both players have complete information; nothing is hidden (unlike Stratego or many card games)
• Two players (sometimes called Left and Right) usually alternate moves (repeat and skip moves are okay; no simultaneous moves)
• The game can end when a pattern is formed, a capture happens, someone runs out of moves, or the board fills

Strong Solutions and Perfect Play #

What the program does in the clip below is a bit like what we do in GamesCrafters: it explores all possible moves and ways a game could play out to find the best strategy.

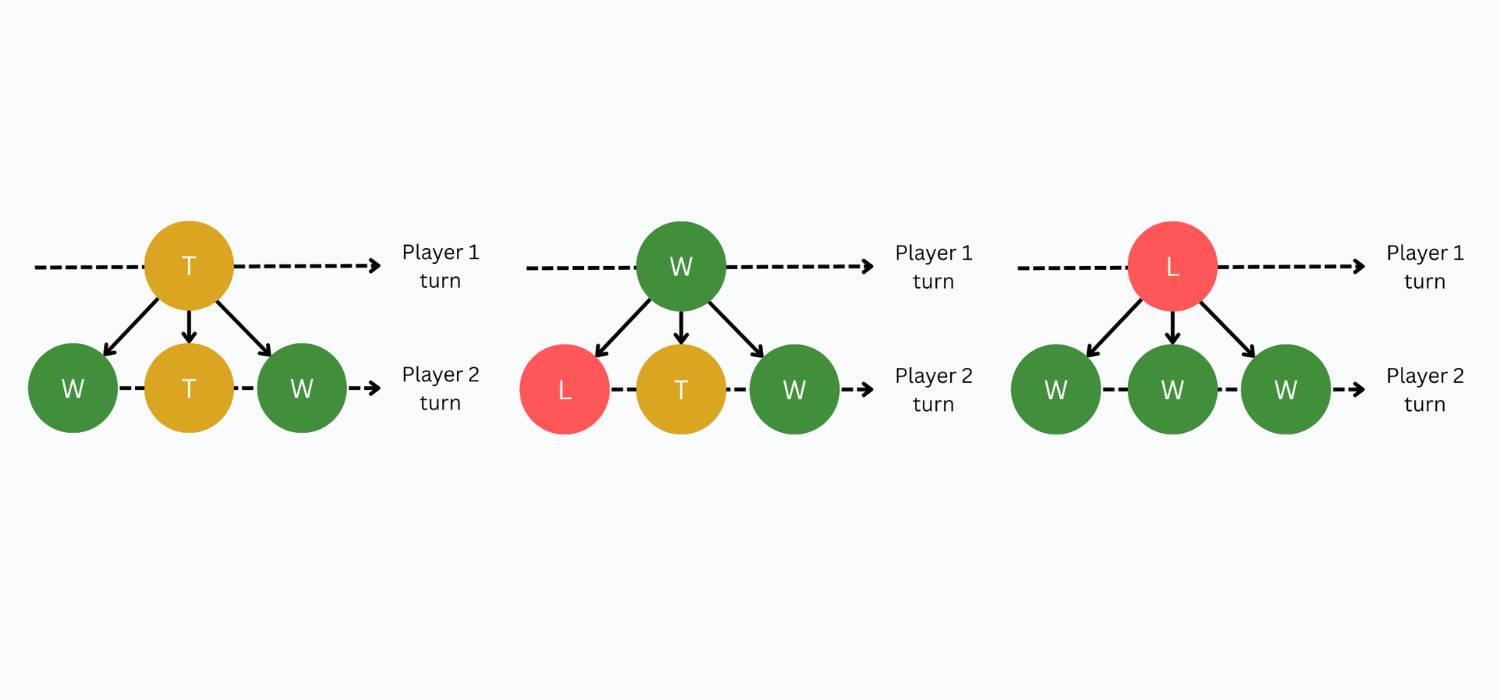
To solve a game, we want to know the outcome of every position under perfect play from both sides. For each position, we assign a value for the player whose turn it is:

• WIN: this player can force a win, no matter what the opponent does
• LOSE: if the opponent plays optimally, this player is doomed
• TIE / DRAW: neither player can force a win with perfect play

We can also track remoteness, which looks at how many moves remain until the game ends, assuming optimal play from both sides.

Some games that can be strongly solved easily include 10-to-0-by-1-or-2 and Tic-Tac-Toe! We will see how to do this in later chapters.

What Is GamesCrafters? #

GamesCrafters is UC Berkeley’s undergraduate research and development group in computational game theory. Since 2001, over 400 students have participated. We now average about 20 students per semester, working in teams of 2 or more, and many students return to take on senior roles and lead sub-teams.

The group focuses on strongly solving abstract strategy games and puzzles.
We add them to the Gamesman system (GamesmanClassic, GamesmanPy, GamesmanUni), which allows anyone to play against perfect strategy and provides tools for post-game analysis and visualization.

Play our games and puzzles here! So far, we have over 70 puzzles and games in our system.

Looking Ahead #

This textbook will walk you from core game theory concepts to a fully deployed game in the Gamesman ecosystem. In the upcoming chapters, you will learn how to:

• Represent games as game trees
• Assign and compute position values (WIN/LOSE/TIE)
• Solve a game by exploring its tree efficiently
• Hash positions and store them in a database
• Build TUI and GUI frontends
• Plug everything into the Gamesman infrastructure and deploy

Through this process, you will gain hands-on experience with many computer science concepts, including:

• Software engineering practices
• Human-computer interaction
• Data structures and search algorithms
• Discrete math (hashing)
• And much more!

By the end, you’ll have solved a game no one has ever solved before and have a live interactive version online that anyone can explore!